b) f(x) = 1 + x3, -1 < x < 1.
c) f(x) = x2sin(
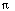 x3), 0 < x < 7.
x3), 0 < x < 7.
Due Thursday, 12 March
The homework due on the final Thursday of the course will not be collected and graded, but you should be prepared to work the following in recitation.
Section 7.4, #10-14,33-36,42
Section 7.6, #4,6,8,10,27,30,33,34
Section 7.7, #1-4,10,11,12,26
Due Thursday, 15 January
To prepare for the test on 16 January, the following problems from Grossman were suggested:
Section 4.2, # 4,6,8,18,20
Section 4.3, # 3,12,21,22,25,26,28
Section 4.4, #11,12,18,19,27,30,33,40
Section 4.5, # 2,6,21,24,28,35
Due Thursday, 22 January
Section 4.6, # 5-8, 27, 33, and the following variant of #33:
F(x) = int(1/(1+t^3), t=x..3);
with
x0 = 1.
Also, students were to do problems at the level of the test I gave in 1995.
Finally, students should know how to plot graphs with Maple and to use the commands diff and int .
Due Thursday, 29 January
Section 4.7, # 18,20,27,38,50
Section 4.8, # 3,4,5
Find the averages of the following functions on the given intervals.
a) f(x) = 1 + x3, 0 < x < 2.
b) f(x) = 1 + x3, -1 < x < 1.
c) f(x) = x2sin(
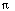 x3), 0 < x < 7.
x3), 0 < x < 7.
Section 5.1, # 8,9,12,20,25
Section 5.2, # 9-14,21,24,25
Work through the Maple worksheet illustrating the important geometric relationships which exist between the graphs of f, the derivative of f and the integral of f. In particular, do the problem at the end of this worksheet.
Due Thursday, 5 February
Section 5.3, #4,5,6,15
Section 5.4, #8,10,20,24
Section 5.5, #3,7,9
Due Thursday, 12 February
To prepare for the test on 13 February, please examine the following on-line materials:
Also, the following problems from Grossman are suggested:
Section 5.6, all drills, and #13-15
Section 8.6, all drills (for review of polar coordinates)
Section 8.7, all drills, and #30,31,36,37,39
Section 6.4, #26-28,43,44
Section 6.6, #6,8,9,17
Section 6.3, #15-19, 25,28,30,31, 38,43
Due Thursday, 19 February
Section 16.2, #2,10,18
Also, work through the Maple worksheet on Growth, decay, and exponential functions, and do the exercises there.
Due Thursday, 26 February
Section 16.3, #3,4,5,17,20,32
Section 16.4, #4,6,8
Also, please work through the worksheet discussing a differential equation for diffusion, and do the exercises there.
To prepare for the test on 3 March, please examine the following on-line materials:
and be prepared to solve any differential equation in Grossman, sections 16.1-16.6.
Due Thursday, 5 March
Section 7.2, # 2,5,14,20,
Section 7.3, #6
A newsgroup called git.math.class.harrell has been created on the Georgia Tech computer system. Please use it to post questions and comments for the other students or the professor.
THIS PAGE IS NOT A PUBLICATION OF THE GEORGIA
INSTITUTE OF TECHNOLOGY AND THE GEORGIA INSTITUTE
OF TECHNOLOGY HAS NOT EDITED OR EXAMINED
THE CONTENT. THE AUTHOR(S) OF THE PAGE ARE SOLELY
RESPONSIBLE FOR THE CONTENT.