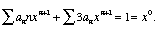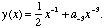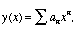 so that
so that
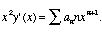 Notice I don't say what power the series begins with. Next plug:
Notice I don't say what power the series begins with. Next plug:
What was the problem, and what can be done about it? The cause of the problem is the factor x2 in front of the derivative, which made it tricky to solve for the power-series coefficients when you plug in. If you did solve the equation with an integrating factor, you found a function which blows up at x=0, so in fact it does not have a Taylor series.
You can still solve the problem with power series, if you are careful. Here is how it goes:
Suppose that
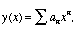 so that
so that
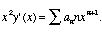 Notice I don't say what power the series begins with. Next plug:
Notice I don't say what power the series begins with. Next plug: