NAME:_________________________________
Instructions: Write the answers where indicated (or points will be taken off). You may attach worksheets if they are likely to be helpful: Some credit may be given for a correct method, if it is clearly explained and convincing.
Some possibly helpful integrals done by Maple are given on the last page.
1. Solve Laplace's equation on the rectangular solid {0 < x < 1, 0 < y < 2, 0 < z < 3} with the following boundary conditions.
u(0,y,z) = u(1,y,z) = 0
uy(x,0,z) = uy(x,2,z) = 0
u(x,y,0) = x, u(x,y,3) = 0
Solution.
The product solutions of Laplace's equation which satisfy all the homogeneous boundary conditions are of the form
for n = 1, 2, ... and m = 0,1,2,.... The general solution will be a double Fourier series of the form
As usual, the hyperbolic sines in the denominator are just I chose to make things work out nicely when we check the nonhomogeneous BC, which fort this problem occuirs at z=0. At that boundary we must have:
Here there is a nice simplification, since there is no dependence on y. This means that only the a0 term in the cosine series is different from 0, and we are left with the Fourier sine series
With the help of the integrals done by Maple and the usual formula for the Fourier coefficients, we find that
ANSWER:
2. Suppose that the temperature distribution u(t,x) in a thin rod satisfies
ut = uxx.
The rod lies on the x-axis from 0 to L, and is pefectly insulated at x=0. At the other end,
it is heated so that:
ux(t,L) = exp(-
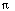 2t/4).
2t/4).
At t=0, the rod is at temperature 10.
HINTS: The following are solutions of the heat equation:
exp(-a2 t) sin(a x)
exp(-a2 t) cos(a x)
a) Solve for the temperature u(t,x) for t>0, 0 < x < L. Begin with L
in the range 1 < L < 2 and then consider the limit as L
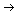 2.
2.
Solution.
The first step is to convert this problem into one with homogeneous boundary conditions. We can do this by defining
as suggested in the hint. This function satisfies the heat equation and has homogeneous Neumann boundary conditions
vx(t,0) = vx(t,L) = 0.
Its initial condition is:
The general solution for v uses a Fourier cosine series:
where the coefficients am are the Fourier cosine coefficients for the initial condition.
A calculation with the standard formula shows that
and
The solution for u is thus:
The first term and the n=1 term both become singular as L
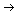 2, but their sum
has a finite limit, which can be calculated with l'Hôpital's rule. The
result is:
2, but their sum
has a finite limit, which can be calculated with l'Hôpital's rule. The
result is:
b) At what values of t,x for 0
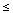 t
t
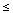 100, 0
100, 0
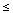 x
x
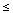 L is the
temperature maximal? At what values of t,x in
these ranges is it minimal?
L is the
temperature maximal? At what values of t,x in
these ranges is it minimal?
Solution.
This question requires the maximum principle, and the observation that heat enters at x=L.
tmax,xmax = 100,L
tmin,xmin = 0,0
c) What is the equilibrium temperature in the rod when t
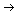
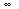 ?
?
Solution.
This can either be read off the solution from part a) or else we can recall that the total heat in the rod is
so
Integrating this gives
Since the equilibrium temperature is a constant, it is the coefficient of L in this expression.
> int(x*sin(n*pi*x/L), x=0..L);
2
L (-sin(n pi) + n pi cos(n pi))
- --------------------------------
2 2
n pi
> int(x*cos(n*pi*x/L), x=0..L);
2 2
(cos(n pi) + n pi sin(n pi)) L L
------------------------------- - ------
2 2 2 2
n pi n pi
> int(x^2 *sin(n*pi*x/L), x=0..L);
3 2 2 3
L (n pi cos(n pi) - 2 cos(n pi) - 2 n pi sin(n pi)) L
- ------------------------------------------------------ - 2 ------
3 3 3 3
n pi n pi
> int(x^2 *cos(n*pi*x/L), x=0..L);
3 2 2
L (n pi sin(n pi) - 2 sin(n pi) + 2 n pi cos(n pi))
- ------------------------------------------------------
3 3
n pi