- Solving on characteristics. The characteristic equations are:
-
Solving by constants of the motion. By looking at the solutions from
part (i), we see that one constant of the motion is
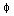 1, for instance
to get
1, for instance
to get
-
Solving an initial-value problem, for instance of the form
-
u(t,t) = g(t):
-
The characteristic equations are
Having this, it is not necessary to solve the characteristic equations
themselves, but in case you want to, you can substitute into them from these
cosntants of the motion. For instance, (x-y) u can be rewritten entirely in
terms of u and the constants
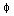 by using:
by using:
-
x+y+u = xyu.