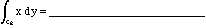
1 (5 points). Evaluate the line integral
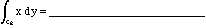
if C2 is the path from (0,0) to (pi/2, 1) along the curve y = sin(x)
KEY FORMULA OR METHOD (optional for partial credit)____________________
_________________________________________________
2 (5 points).
a) Is the vector field

Exact? _____Yes______No
b) If your answer to a) is Yes, find a scalar field f such that F = --f. If your answer to a) is No, calculate the integral of F around the counterclockwise circle of radius 2, centered at the origin.
ANSWER: __________ = _________________________________________
c) Evaluate the closed loop integral
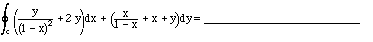
if C is the counterclockwise circle of radius 2, centered at the origin.
HINT: See if the answers to a) and b) help.
KEY FORMULA OR METHOD (optional for partial credit)____________________
_________________________________________________
4 (5 points). Let R be the solid region inside both the sphere x2 + y2 + z2 = 4 and the cone z = r(x2 + y2). Let the density be f(x,y,z) = z. Set up an explicit integral for the total mass u and evaluate it:
The coordinates I am using are known as __________________coordinates.
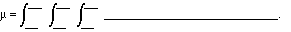
The value of this integral is:
u = _____________________________
KEY FORMULA OR METHOD (optional for partial credit)____________________
_________________________________________________