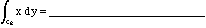
1 Evaluate the line integral
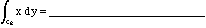
if C2 is the path from (0,0) to ( \pi /2, 1) along the curve y = sin(x)
2. Let F(x,y,z) := x i + (y+z) j+ (z2+y) k.
a) Is this vector field exact ? ____Y____N. Give the calculation(s) necessary to answer this question here:
b) Evaluate
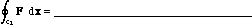
where C1 is the closed loop given by x(t) = 3 + cos(t), y = 2 - 2 sin(t), z = t^2 - 2\pi t,
0 <= t <= 2 \pi .
c) Evaluate
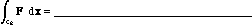
where C2 is the non-closed curve given by x(t) = 3 + cos(t), y = 2 - 2 sin(t), z = t^2 - 2\pi t, 0 <= t <= \pi .
3. Evaluate the closed loop integral

4. Consider the surface x(u,v) = u cos(v), y(u,v) = - u sin(v), z(u,v) = v, 0 <= u <= 1, 0 <= v <= \pi /3. In case it is useful, note that z = - arctan(y/x). (SEE INTEGRAL TABLE)
a) A normal vector to the surface at a particular point is given by N = ________________.
b) The surface area element is: d\sigma = _________________________________
c) The integral for the area in question is: Area = _____________________________
d) The value of the area is Area = ______________________________________