Linear Methods of Applied Mathematics
Evans M. Harrell II and James V. Herod*
version of 8 August 1996
The physics and mathematics of the vibrating string were studied by Jean le Rond d'Alembert, and later by Joseph Louis Lagrange, Leonhard Euler, and Daniel Bernoulli, who gave a satisfactory discussion of the physics of the vibrating string. I have not been able to locate a detailed discussion of Bernoulli's derivation of the wave equation, but it is likely that he based it on an energy principle, somewhat as follows. First let us recall that in classical mechanics, Newton's equations for the motion of a particle are equivalent to the vanishing of the first variation of the Lagrangian action integral,
The kinetic energy is usually of the form
 ) = (q(t) +
) = (q(t) +
 h(t)),
h(t)),
 ), then
), then
 and
retain only the first-order term, the stationary condition becomes
and
retain only the first-order term, the stationary condition becomes
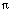 t/L), with L = t1-t0, we see that the only possibility is for
t/L), with L = t1-t0, we see that the only possibility is for
The big advantage of Lagrangian mechanics is that it allows us relatively
easily to find the equations of motion of an extended body, such as a string.
Suppose now that we have a taut string along the x-axis between positions a and
b, but displaced laterally by an amount u(t,x). If the density is
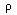 ,
then the kinetic energy of a small bit of string at position x is
,
then the kinetic energy of a small bit of string at position x is
 h(t,x),
h(t,x),
h(t,a) = h(t,b) = 0. The action is a double integral,
 Lagrange's condition reads:
Lagrange's condition reads:
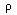 and T := 2 F' are constants. If we integrate the first integrand by
parts in the t variable and the second by parts in the x variable, we now find
that:
and T := 2 F' are constants. If we integrate the first integrand by
parts in the t variable and the second by parts in the x variable, we now find
that:
If h is arbitrary enough to run through a complete set, we must conclude that
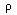 a positive constant with dimensions of
velocity2.
a positive constant with dimensions of
velocity2.Judging from guitar strings, for which a 1 meter taut string gives a musical note in the mid range of the musical scale, typical values of c for thin metal strings are on the order of 1000 m./sec. The wave equation (WE) also describes one-dimensional acoustic waves (c ~ 344 m/sec. in air at room temperature or 330 m./sec. at 0 C) and light waves (c ~ 300,000,000 m./sec.), although the physical derivation in these cases is very different.
Return to Chapter VI
Return to Table of Contents
Return to Evans Harrell's home page