Linear Methods of Applied Mathematics
Evans M. Harrell II and James V. Herod*
version of 11 May 2000
(Some remarks for the instructor).
We begin with the case of the first Fredholm alternative. If the equation is in this case, we are guaranteed that it has a unique solution - but how to find it?
Our method to solve a nonhomogeneous differential equation will be to find an integral operator which produces a solution satisfying all given boundary conditions. The integral operator has a kernel called the Green function , usually denoted G(t,x). This is multiplied by the nonhomogeneous term and integrated by one of the variables.
There are several methods of constructing Green functions. The one we will present first, and emphasize, is the one students seem to prefer. Perhaps this is because it is easy to remember and has an inherent simplicity. Other methods will be included in these notes for comparison. There are ideas which the other methods use that are important.
As before, we assume a certain form for the differential operator L:
We suppose that an(x) is not zero on [0,1] and that each term of the sequence ap(x), p=0,..., n, has at least n continuous derivatives. We discuss the construction of the Green function in three cases depending on the nature of the boundary conditions. Until further notice, we assume the first alternative holds and will repeat this warning for emphasis. We continue to denote M and M* as the manifolds associated with {L,B} and {L*,B*}, respectively.
In most of our examples, and in the majority of applications, the differential equations are of second order. Ultimately, this arises from Newton's force law, F = m a, which is second order, since acceleration is a second derivative.
Let's begin by describing the algorithm for constructing G for second-order problems. We'll discuss why this works below
The function G depends on two variables and has the following properties: if t is in (0,1) , then
exists for 0 < x < t and for t < x
< 1. Further suppose that these derivatives have a continuous extension to
the triangular region 0
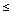 x
x
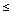 t and t
t and t
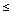 x
x 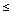 1. The effect of
this extension is that
1. The effect of
this extension is that
and
for p = 1,2
At the boundary we shall insist that G(x,t) be continuous. For the partial Gx, however, we require a special jump discontinuity as follows:
Here is what happens if there are derivatives of higher orders:
The function G should be constructed on [0,1]x[0,1] to have the following properties:
exists for 0 < x < t and for t < x
< 1.
Further suppose that these derivatives have a continuous extension to
the triangles 0
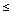 x
x 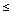 t and t
t and t
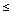 x
x 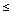 1.
1.
and
At this point, all we have asked of G is that it should have n
continuous partials on the closed triangles 0 < x < t
and t < x < 1. The requirement along the boundary will be
that for p
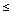 n-2, we have continuity. For example at p = 0, the effect is
that G(t+,t ) = G(t-,t). Indeed, G(t+,t) =
G(t,t-) = G(t,t+) = G(t-,t). And, this
happens for the pth partials up to p = n-2. For the (n-1)th
partial, we allow a jump discontinuity as prescribed in the summary
below:
n-2, we have continuity. For example at p = 0, the effect is
that G(t+,t ) = G(t-,t). Indeed, G(t+,t) =
G(t,t-) = G(t,t+) = G(t-,t). And, this
happens for the pth partials up to p = n-2. For the (n-1)th
partial, we allow a jump discontinuity as prescribed in the summary
below:
xn-1
= 1/an(t).">
Before showing that the above recipe really does provide solutions to the nth order equation, it would be well do to some examples, beginning with
Model Problem XVI.1. (First alternative, initial conditions): Given f continuous on [0,1], construct y such that
We are in the first alternative because for this {L,B1,B2} the system L(y) = 0, B1(y) = B2(y) = 0 has only one solution and it is zero. We construct G step-by-step from the above directions.
To follow the directions of step (a) we need the general solution of the homogeneous equation L(y) = 0, that is, we need the general solution of the homogeneous equation
Note that A, B, C, and D are constant in x, but may change with t. We chall determine the four unknowns from the continuity and jump conditions.
To follow the directions of step (b), which requires that G(.,t) be in M, we need
To follow the directions of step (c), which requires that G(t+,t) = G(t-,t), we need
The problem has been reduced to a matrix equation! We have solved the equations to find A = 0, B = 0, c = -e2t, and d = et. The end result is:
We are confident that if f is continuous then the equation y = Gf provides a solution for L(y) = f because of Exercise 5 of Chapter XIII .
A DIRECT VERIFICATION THAT THIS METHOD GIVES SOLUTIONS FOR SECOND ORDER EQUATIONS
Suppose that L(y)(x) = a2(x)y''(x) + a1(x)y'(x) + a0(x) y(x). Let
Since G( , t) is in M then u is in M. It remains to see that L(u) = f. Note that
This last equality holds because of the assumption that G(x,x-) = G(x,x+).
Also,
This last equality uses the condition Gx(x,x-)) - Gx(x,x+)) = 1/a2(x). Finally, we use the fact that G(x, t), as a function of x, satisfies L(y) = 0 on [0,x] and on [x,1] to get that L(u) = f.
Model Problem XVI.2 ( first alternative; unmixed, two point boundary conditions):
We shall construct the Green function for the problem
A little bit of work needs to be done to verify that we are in the first alternative. If L(y) = 0, then there are numbers a and b such that
The construction for G is as before:
The two boundary conditions and the continuity conditions lead to the equations
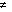 0
0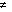 0 and u2(1) = 0.
0 and u2(1) = 0.
Now, make up G this way,
Apply the boundary conditions:
The continuity conditions give the two equations
is called the Wronskian of u0 and u1.
Here is the final result:
There is one more important piece of information that you will learn, or be reminded of, if we work out both parts of the formula for G. Recall that
And now, to compute w(t). The chore of that computation seems too tedious to be fun. Not to worry! Look up "Wronskian" is some good sophomore differential equations book and you will find a convenient formula :
(16.1)
Now the computation is easy:
and w(t) = (e2 - e1)e-3t.
Hence
and
We got more from this example than the answer: we also got the following quick method that works for problems of this type:
Pick u1 and u2 such that B1(u1) = 0,
B2(u1)
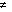 0, B2(u1) = 0, and
B1(u2)
0, B2(u1) = 0, and
B1(u2)
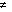 0.
0.
Then
where w is the Wronskian of u1 and u2.
Model Problem XVI.3. (first alternative; mixed, two point boundary conditions):
Suppose
Since also
These two equations imply that a = b = 0. We now begin the construction of the Green function.
Pick 0 < t < 1:
We have four constants to determine; here are four equations:
 (x - t).
(x - t).
By now you should believe that except for arithmetic details, you can work any of these problems. We have come to the place where we need to get this problem into perspective.
We know that the requirements of Chapter XV give the Kronecker delta symbol,
for any vector v.
Thus A G = Id in components becomes
When trying to solve differential equations, we might hope to find
G(.,t) as a solution to the equation L(G(.,t)) =
 (.,t). Some understanding
of this equation is in order for the right side is not a function in the
ordinary sense. As has already been pointed out, it is a "generalized
function". The analogy with the matrix problem is pretty close: The delta
function in essence gives the continuous coordinates of the identity
operator:
(.,t). Some understanding
of this equation is in order for the right side is not a function in the
ordinary sense. As has already been pointed out, it is a "generalized
function". The analogy with the matrix problem is pretty close: The delta
function in essence gives the continuous coordinates of the identity
operator:
for any a,b with a < x < b. Recall that the integral is a sort of continuous sum, so this is appropriate.
We present here, not a proof, but an understanding that
 (x - t).
(x - t).
(16.2)
Suppose that
and that equation (16.2) holds. Intuition is a guide:
If one were asked to solve the equation L(y) = f, where L is a reasonable second order operator, in the context of a sophomore differential equations course, one would think of the variations of parameter formula. In that setting, and for second order problems with u0 and u1 linearly independent solutions of the homogeneous equation,
and
This suggests an interpretation for "solution" of the second order equation:
 (x,t).
(x,t).
As above, the distribution equations should have solution
Theorem XVI.4. If, for each t, G(.,t) is in M and L(G(.,t))(x) =
 (x,t) then G satisfies the
four equations of Chapter XV.
(x,t) then G satisfies the
four equations of Chapter XV.
Proof. We hope to recognize the four equations which we used to define G for second order problems as arising from the above requirements for G. Two of those equations come from asking that G(.,t) should satisfy the two boundary equations. One other, G(t+,t) - G(t-,t) = 0, comes from the requirement that G(.,t) should be continuous. To derive the equation
Gx(t+,t) - Gx(t-,t) = 1/a2(t),
we first compute Gx(x,t).
Gx(x,t) =
= C0,x(x,t) u0(x) +
C0(x,t) u0'(x) + C1,x(x,t) u1(x)+
C1(x,t) u1'(x)
= C0(x,t) u0'(x)
+ C1(x,t) u1'(x).
This last equality follows from (b). To find
In a similar manner,
Hence, the inverse of the differential operator L on the set M is obtained by finding the function G( ,t) in M which satisfies (16.2),
 (x-t).
(16.3)
(x-t).
(16.3)
QED
We now discuss the problems where the Second Alternative holds. The supposition is that there is a nontrivial solution for L(y) = 0, B1(y) = B2(y) = 0. The Fredholm Theorems assure us that, if f is continuous, then there is a solution for L(y) = f, with B1(y) = B2(y) = 0 provided
for all solutions w of the equation L*(w) = 0, B1*(w) = B2*(w) = 0. As before, we will construct Green functions G such that, in case f satisfies the above requirement, then
provides a solution for L(y) = f.
In this second alternative, there may be many solutions for the equation L(y) = f. Consequently, we expect there may be many Green functions. In the technique developed below, G( ,t) is always in
We again divide the problems into three cases according to the nature of the boundary conditions. We shall illustrate methods of construction.
The first case to consider is where the boundary conditions arise as initial conditions. This case is not pertinent for the initial value problem has a unique solution. Thus, case one is always in the first alternative.
Model Problem XVI.5. (Second Alternative,unmixed, two point boundary conditions)
Suppose that L(y) = y'' + y' - 2y, B1(y) = y(0) - y'(0), and
B2(y) =
y(1) - y'(1). It is the purpose of this example to show that there is no
function G such that L(G(.,t))(x) =
 (x,t). Note that L*(z) = z'' - z' -2z
and M* = {y: 2z(1) = z'(1), 2z(0) = z'(0)}. Nontrivial functions in the
nullspace of {L*, B1*, B2*} are multiples of e2t.
Hence, we are in the second alternative. The Fredholm Alternative
theorem suggests that there will be no function G such that, if t is
in (0,1), then the distribution equation L(G( ,t)) (x) =
(x,t). Note that L*(z) = z'' - z' -2z
and M* = {y: 2z(1) = z'(1), 2z(0) = z'(0)}. Nontrivial functions in the
nullspace of {L*, B1*, B2*} are multiples of e2t.
Hence, we are in the second alternative. The Fredholm Alternative
theorem suggests that there will be no function G such that, if t is
in (0,1), then the distribution equation L(G( ,t)) (x) =
 (x,t)
holds unless
(x,t)
holds unless
Of course, the value of this integral is not zero.
For this situation, we must modify the construction of the Green function.
INDICATION OF PROOF. By the Fredholm Alternative Theorems, there will be such a function G provided
for all w in the nullspace of L*. This can be verified by writing w in terms
of this orthonormal basis ,
and
evaluating the dot product.
How to construct G such that
First, find linearly independent solutions yp, p=1,...,n, of the homogeneous equation L(y) = 0. Then, find solutions up, p=1,..., m < n, for the equations L(up, p=1,...,)(x) = vp, p=1,...,(x). It is not required that these solutions should satisfy any special boundary conditions.
The problem of finding G is now a problem of finding constants Cp and Dp such that
The constants Cp and Dp are determined by these 2n equations:
CONTINUATION OF THE PREVIOUS EXAMPLE
Recall that L(y) = y'' +y' -2y, B1(y) = y(0) - y'(0), and B2(y) = y(1) -
y'(1). Linearly independent solutions for L(y) = 0 are e-2x and
ex. A normalized basis for the one-dimensional nullspace of
{L*,B1*,B2*} is
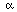 e2x where
e2x where
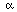 is the positive number
given by
is the positive number
given by
A solution u for the equation y'' +y' -2y =
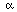 e2x is
u(x) =
e2x is
u(x) =
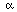 e2x/4.
e2x/4.
Now, G is given by:
The four constants - A,B,C, and D - can be solved by these four equations:
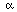 2et/4
2et/4
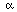 2e2t/12, C = Ae4, D-B =
e-t/3.
2e2t/12, C = Ae4, D-B =
e-t/3.
QED
Example XVI.7. (Second Alternative, mixed, two point boundary conditions.)
Suppose that L(y) = y'', B1(y) = y(0) + y(1), B2(y) = y'(0) - y'(1). Then L*(z) = z'', B1*(z) = z(0)- z(1), B2*(z) = z'(0) + z'(1). All solutions of {L,B1, B2} are multiples of 2x - 1 . A nontrivial solution of [L*,B1*, B2*} is the constant function 1. Also, the function V(x) = 1 forms a basis for the null space of 0 = L*(z) in M*. The function u(x) = x2/2 satisfies L(u) = 1. Thus
G(x,t) = BLC{(A(A + Bx - x2/2 if x < t,C + Dx - x2/2 if t < x.))
We have four unknowns; we have the following four equations:
(Review the general method or ad hoc method for constructing Green functions.)
(a) L(y) = y''
(b) L(y) = y'' +
4 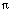 2y
2y
(c) L(y) = 2y'' + y' - y
(d) L(y)(x) =
(exy'(x))'.
(Answers)
satisfies L(u) = 0, u(0) = 0, and u'(0) = 1/a2(t). Let H(x,t) = 0 if x < t and = u(x-t) if t < x. Show that H is a Green function for the problem {L, B1(y) = y(0), B2(y) = y'(0) }.
and H(x,t) be the function given by H(x,t) = G(x,t) b(t) (Note: Here H is not the Heaviside function). Show these are equivalent:
(a) y''(x) - b(x)y(x) = f(x), y(0) = y'(0) = 0, and
(b) L(y) =4y'' - y, B1(y) = y(0) - 2y'(0), B2(y) = y(1) - 2y'(1).
(c) L(y) = y'' - 2y' - 3y, B1(y) = 3y(0) - y'(0), B2(y) = 3y(1) - y'(1).
(a) L(y) = y'', B1(y) = y(0), B2(y) = y(1),
(b) L(y) = y'', B1(y) = y(0) + y'(0), B2(y) = y(1) + y'(1).
(c) L(y) = y'', B1(y) = y(0) + y'(0), B2(y) = y(1) - y'(1),
(d) L(y) = y'' + 4 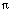 2y, B1(y) = y(0) + y'(0), B2(y) = y(1) -
y'(1).
2y, B1(y) = y(0) + y'(0), B2(y) = y(1) -
y'(1).
(e) L(y) = 2y''+ y'- y, B1(y) = y(0) + y'(0), B2(y) = y(1) - y'(1).
(f) L(y)(x) = (ex y'(x))', B1(y) = y(0) + y'(0), B2(y) = y(1) - y'(1).
(Answers)
solves
L(u) = f.
Notice that the integral is the same as <G(x,t),f(t)>, if the inner product is calculated with t as the integration variable.
 (x) is an even function, in the sense
that
(x) is an even function, in the sense
that
 (-x) =
(-x) =
 (x). (Use a change of variables.)
(x). (Use a change of variables.)
u''(x) - u(x) = f(x).
Since the boundary conditions have not been specified, there will be many Green function for the differential equation
u''(x) - u(x) = f(x), u(0) = u(1) = 0.
(a) Classify G(x,t) as an integral kernel as in Chapter XII. Is it separable? Is it small (in either sense)?
(b) Discuss how one could solve the integral equation
with the methods of Chapter XII. To what differential equation is it equivalent?
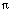 2y, B1(y) = y(0) - y(1), B2(y) = y'(0) +
y'(1),
2y, B1(y) = y(0) - y(1), B2(y) = y'(0) +
y'(1),
(a) L(y) = y'',
(b) L(y) = 2y'' + y' - y,
(c) L(y) = y'' + 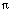 2y
2y
(d) L(y) = y'' + 4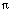 2y
2y
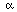 , B2(y) =
, B2(y) =
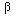 , first
construct G for the problem L(y) = f, B1(y)= 0, B2(y) = 0. Then construct
functions z1 and z2 such that B1(z1) = 0, B2(z1) != 0, and B1(z2) != 0, B2(z2)
= 0. The solution for the original problem is
, first
construct G for the problem L(y) = f, B1(y)= 0, B2(y) = 0. Then construct
functions z1 and z2 such that B1(z1) = 0, B2(z1) != 0, and B1(z2) != 0, B2(z2)
= 0. The solution for the original problem is
QED
(a) u(0) = u(1) = 0.
(b) u(0) = u'(0) = 0.
(c) u(0) = 3, u(1) = 5,
(d) u'(0) = 3u(0), u'(1) = 5 u(1),
(e) u(0) = u(1), u'(0) = u'(1),
(f) u(0) = 3, u'(0) = 5,
(g) u'(0) = 3, u(0) = 5,
(h) u(0) = 0, I(0,1, ) u(x) dx = 0.
(answers)
(a) u(0) = 3, u'(1) = 5.
(b) u(0) - u'(0) = 3, u(1) = 5.
(a) Find conditions on f in order that u'' + 4
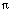 2 u = f,
u(0)=u(1), u'(0) = u'(1) should have a solution.
2 u = f,
u(0)=u(1), u'(0) = u'(1) should have a solution.
(b) Give the Green function for this problem.
(c) By finding the Green function for the problem L(y) = y'', y(0) = y(1), y'(0) = y'(1), re-write this equation as an integral equation such as was studied in the previous chapter.
L(y)(x) = (ex y' )' and B1(y) = y(0), B2(y) = y'(0).
(a) Show that (ex y')' z - y (exz')' = [ ex (z y' - z' y)]'.
(b) Give L* and B*.
(c) Give the Green function for the problem L(y) = f with B1(y) = B2(y) = 0.
(d) Rewrite the problem (ex y')' + sin(x) y(x) = f(x) , y(0) = y'(0) = 0 as an integral equation in the form
y = K(y) + F.
Be sure to identify K and F carefully.
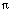 ] and
] and
y(0) = 0 = y(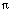 ).
).
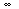 < x <
< x <
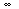 .
.
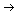
 .
.