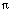 n x/L rather
than all integer multiples of
n x/L rather
than all integer multiples of 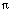 x/L. We shall also discuss an
"exponential" Fourier series,
which uses complex functions of the form
x/L. We shall also discuss an
"exponential" Fourier series,
which uses complex functions of the form
Linear Methods of Applied Mathematics
Evans M. Harrell II and James V. Herod*
version of 26 December 1995
There are three distinct versions of the Fourier
series in common use, the "full"
Fourier series, the Fourier sine series, and the Fourier cosine series.
They are based on slightly different choices of an orthogonal basis set, whether
(2.6) for the Fourier sine series,
(2.7) for the Fourier cosine series, or
(2.8) for the full Fourier series. Notice that while the
full set (2.8) contains both sines and cosines, it does not contain as many frequencies
as either of the other sets, since the trig functions depend on 2 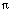 n x/L rather
than all integer multiples of
n x/L rather
than all integer multiples of 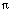 x/L. We shall also discuss an
"exponential" Fourier series,
which uses complex functions of the form
x/L. We shall also discuss an
"exponential" Fourier series,
which uses complex functions of the form
exp( 2 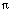 i x/L),
i x/L),
but this is actually the same series as the full Fourier serie: It has simply been written in a convenient way using exponential functions.
The three different sets do an equally good job of approximating functions in the r.m.s. sense, but their relationship to symmetries is different. For this reason, different sets of Fourier functions will arise in our study of partial differential equations, depending on which kind of "boundary conditions" which are physically appropriate for a given problem.
The full Fourier series consists of functions which are periodic , and are
particularly good for representing or approximating periodic functions, that is,
functions for which f(x + L) = f(x). Examples include sounds built on a basic
frequency with overtones or a physical function depending on an angular variable
such as longitude. The Fourier cosine series, in contrast, is well adapted to functions
which have zero derivatives at x=0 and x=L, since all the functions
cos(n 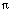 x/L) have this property.
A related but less obvious property that begs for the use of cosine functions is an
even symmetry: f(-x) = f(x). If the function you wish to approximate is an even function,
then the cosines are a good candidate for a basis set. Notice that the cosines are not only
even under reflection about 0, but also about the other end of the interval, x=L.
Fourier sine series are better suited for odd functions.
A
Fourier cosine series represents a function as
x/L) have this property.
A related but less obvious property that begs for the use of cosine functions is an
even symmetry: f(-x) = f(x). If the function you wish to approximate is an even function,
then the cosines are a good candidate for a basis set. Notice that the cosines are not only
even under reflection about 0, but also about the other end of the interval, x=L.
Fourier sine series are better suited for odd functions.
A
Fourier cosine series represents a function as
x/L)">
(3.b1)
for 0 < x < L. In most applications a = 0 < x < L, but this is not strictly necessary.
If the lower limit for x is a > 0, then the Fourier cosine series can still be used
if we change variables from x to x-a, so the basis functions are
cos (m pi (x-a)/L).
The formulae for the coefficients a_m are the same as in
(2.12) and (2.13), except that the Fourier cosine series
uses all integer multiples of 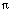 x/L, where L=b-a, not just the even multiples:
x/L, where L=b-a, not just the even multiples:
while for m>0,
x/L)">
(3.b2)
Just as for the full Fourier series, the Fourier sine functions are a
complete set, and they satisfy some useful
identities, which I have collected in a theorem (which is almost identical
to
the one for the full series).
Historically,
parts of this theorem were contributed by Fourier,
Parseval,
Plancherel,
Riesz,
and
Fischer,
and in most sources it is considered several theorems. For proofs
and further details, refer to Rudin's Real Analysis or Rogosinski's
Fourier Series .
The powerful theorem behind the Fourier cosine series III.3b.
If f(x) is square-integrable on an interval [a,b], then
a) All of the coefficients am of (3.b2) are well defined.
b) All of the coefficients am are uniquely determined by f(x) and depend linearly on f(x).
b) The series
converges to f(x) in the mean-square sense. In other words,
We shall express this by writing
(Remember, however, that this series converges in a mean sense, and not necessarily at any given point.)
d)
and the right side is guaranteed to converge.
e) If g is a second square-integrable function, with Fourier cosine coefficients a-tilde, then
This is known as the Parseval formula for the Fourier cosine series.
Conversely, given a square-summable sequence a_m, i.e., real or complex numbers such that
is finite, they determine a square integrable function f(x) uniquely a.e. such that all the statements of this theorem hold.
In addition, if f(x) is piecewise continuous, then Theorem III.6 likewise holds, except at the end points of the interval. If 0 < x < L, the Fourier cosine series will converge to the average of the right and left limiting values of f at x. When x=0 or L, however, the Fourier cosine series will always converge to the one-sided limit of f at that point.
When we study partial differential equations beginning in
chapter VI, Fourier sine or cosine
functions will arise depending on the
boundary conditions.
If we know that the functions we seek are equal to 0 at the
end points 0 and L, then we can ensure this fact by writing
them as sums of sines of the form
sin(n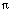 x/L).
Similarly, if we know that the derivatives are equal to 0 at the
end points, we can accomplish this with a sum of cosines of the form
cos(m
x/L).
Similarly, if we know that the derivatives are equal to 0 at the
end points, we can accomplish this with a sum of cosines of the form
cos(m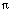 x/L).
x/L).
Compare with the Fourier sine series
Compare with the full Fourier series
Compare with the exponential Fourier series
Return to Table of Contents
Return to Evans Harrell's home page