Past homework assignments

Due Thursday, 25 August

• Evans, Chapter 1 and Sections 2.1-2.2
• Read a derivation of the wave equation that correlates with the one in the first lecture.
• Review the lecture from 23 August

• Section 1.5, #1 (and optionally 2-4 to help you want to understand multiindices)
• (Refer to the derivation of the wave equation for this problem.) Derive a wave equation for the vibrating string if the x-axis is horizontal and we take gravity into account. The gravitational potential energy of the string is where g, the gravitational constant, is approximately 980 in the cgs system. Assume that the mass density is equal to 1.

Due Tuesday, 13 September

• Evans, Sections 2.2, 2.4, Appendix C4.
• Review the lecture from 25 August
• Review the lecture from 6 September
• Review the lecture from 8 September

• Section 2.5, #1, 4

Due Tuesday, 20 September

Reading:

• Evans, Sections 2.2-2.4.
• Review the lecture from 8 September
• Review the lecture from 13 September
• Review the lecture from 15 September

• Solve Laplace's equation on the rectangle 0 < x < 1, 0 < y < 4, with conditions that
  u(x,0) = 2, u_y(x, 4) = 0, u(0,y) = sin²(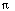y), u(1,y) = 0.
• Evans, Section 2.5, #5.

Due Tuesday, 27 September

Reading:

• Evans, Sections 2.2-2.4.
• Evans, Section 4.3.1 (on the Fourier transform)
• Review the lecture from 15 September
• Review the lecture from 20 September
• Review the lecture from 22 September

• Prepare the take-home portion of the test
• Do Exercise 6 of H&H, chapter 19
• Find the fundamental solution (Green function for equation on R³) for the equation
  -(D₁² + D₂² + 4 D₃³ - D₁ +(1/4)) u = f.
  You are permitted to make a formal derivation, using delta functions. Two strategies you might consider are a) reducing the problem to a known one; and b) Fourier transform.

Due Tuesday, 4 October

• Evans, Sections 2.3-2.4.
• Review the lecture from 27 September

None, because of the test on the 29th.

Due Tuesday, 11 October

• Evans, Sections 2.3-2.4.
• Review the lecture from 4 October
• Review the lecture from 6 October

• Section 2.5, #10, 13

Due Tuesday, 25 October

• Evans, Sections 4.3.1, 3.2.
• Review the lecture from 11 October
• Review the lecture from 13 October
• Review the lecture from 20 October

• Section 4.7, #4
• Calculate the Fourier transforms of xⁿ exp(-x²/2) for n = 0 ... 4, and use the result to find at least five eigenfunctions functions h_n(x) of the differential operator -D² + x². In this exercise x is a one-dimensional variable, and D = d/dx.
• Solve the heat equation u_t = u_xx for t > 0, e- infinity < x < infinity, with initial conditions u(x, 0) = 2 + 3x + 2 x³ - 6 x⁴

Due Tuesday, 1 November

• Evans, Sections 3.1, 3.2.
• Review the lecture from 25 October
• Review the lecture from 27 October

• Consider the first-order PDE x u_x - y u_y + u = x.
  1. Determine the characteristic traces (= "projected characteristics")
  2. Find two independent functions of x,y,z that are constant along characteristics.
  3. Find the general solution of the PDE, preferably as an explicit function of x,y.
  4. Solve the Cauchy problem for the PDE with initial condition that u(x,y) = x on the curve y = x². Comment on the domain of influence of this initial curve, if appropriate.
• Answer the same questions for (u - y)u_x - y u_y = (x - y)
• Section 3.5, #3 (b) and (c).

  Sample solutions

Due Tuesday, 8 November

• Evans, Sections 3.4.
• Review the lecture from 1 November
• Review the lecture from 3 November
• Review the sample solutions linked below for the last two sets of exercises.

• Answer the questions from last week for the following first-order PDEs:
  1. (1/x) u_x - (1/y) u_y = x² + y², your favorite initial conditions.
  2. (y+x) u_x + (y-x) u_y = u, your favorite initial conditions.
  3. (x² + y²) u_x + 2 x y u_y = xz, with initial conditions at x=2 that y² + u² = 4
  4. u_x + u_y = u², u(x,0) = x²
  5. u_y = x u u_x, u(x,0) = x.
  6. u_x² - u_y² = 2 u, u(0,y) = (1+y)²
• Chapter 3.5, # 2,3,4

See the solutions

Due Tuesday, 29 November

• Evans, Sections 3.3, 3.4, 4.6 (lightly).
• Review the lecture from 10 November
• Review the lecture from 15 November
• Review the lecture from 17 November
• Review the lecture from 22 November

• Section 3.5, #6, 7 (7 is optional)
• Classify the type of the following second-order PDEs. If the type depends on the variables, state exactly how.
  1. 2 u_xx - 4 u_xy + 3 u_yy - 2 u = 0
  2. y u_xx - 2 u_xy + exp(x) u_yy + sin(x) u_x + u = 0
  3. u_xx + u_yy + u_zz + 2 u_xy + 6 u_yz = 0

  Sample solutions

• For at least two of the equations in the previous problem, exhibit the change of variables that transforms the equation into one where the principal part is in canonical form.

Due Tuesday, 6 December

• Read Prof. Harrell's lecture on asymptotics and perturbation theory
• Evans, Section 4.5 (lightly)
• Review the lecture from 29 November
• Review the lecture from 1 December

• Compare the explicit inverses and perturbation series for (A + 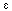B), where

  1. 
     
         [1   0]           [0   1]
     A = [     ],      B = [     ]
         [0   1]           [1   0]
     
     

     Sample solutions

  2. A = -d²/dx² on 0 < x < 1, with Dirichlet conditions at 0 and 1, B = 1. (Optional exercise - for more information on solving ODEs of this type with one-dimensional Green functions, see the sections of my WWW undergraduate textbook with Herod entitled Ordinary differential operators and Finding Green functions for ODEs.)

    THIS PAGE IS NOT A PUBLICATION OF THE GEORGIA
    INSTITUTE OF TECHNOLOGY AND THE GEORGIA INSTITUTE
    OF TECHNOLOGY HAS NOT EDITED OR EXAMINED
    THE CONTENT. THE AUTHOR(S) OF THE PAGE ARE SOLELY
    RESPONSIBLE FOR THE CONTENT.