Mathematics 6321
Complex Analysis
Spring, 2005
Current reading and homework assignments
Due Monday, 2 May
There will be a final exam on this date
Reading
Exercises
-
Find all the conformal maps from the upper half plane to itself.
-
S-S, section 8.5, #3,10,12
-
Show that if the Taylor series
Σk=0
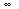 ak zk
has radius of convergence r > 0,
ak zk
has radius of convergence r > 0,
then on the disc
|z| 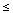 ρ < r,
ρ < r,
Σk=n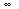 ak zk = O(zn).
ak zk = O(zn).
-
Use Cauchy's integral formula to prove:
Let f(z) be holomorphic in a closed annular sector S
and f(z) = O(zp)
as z tends to infinity in S. Then in any proper annular subsector
C with the same vertex as S, f(m) = O(zp-m).
(By definition, an annular sector is the
intersection of a sector with the
exterior of a disc centered at its vertex.)
-
Find asymptotic expressions for the integrals from 0 to infinity of
-
exp(-t - s ta) tb-1
-
ts exp(-t) log t
and for the integral from 0 to π2/4 of
exp(x cos t1/2).
-
Stay tuned for more suggestions!
Past homework assignments
Review and Historical Comments:
Due Thursday, 20 January
Reading
-
Stein-Shakarchi, chapters 1-2
Lecture pictures
Exercises
Hand in at least 5 of the following, and think about all of them:
-
S-S, section 1.4, #3,7,12, 16 (d) and (e), 19. 25.
-
S-S, section 2.6, #6,10.
Due Thursday, 27 January
Reading
-
Stein-Shakarchi, chapter 2
Lecture pictures
Exercises
-
S-S, section 2.6, #2,9, 12.
Note: Prof. Harrell had jury duty on this date, and the
class was conducted as a problem session.
Due Thursday, 3 February
Nothing - continued from previous week.
Due Thursday, 10 February
There is a scheduled test on this date.
Reading
-
Stein-Shakarchi, chapter 3
Lecture pictures
Exercises
For test preparation, work the problems in
chapters 2 and 3 (at least sections 1-4) of S-S, in particular:
-
S-S, section 2.6, #7,8, 15, which last will
be on the test verbatim
-
S-S, section 2.7, #3
-
S-S, section 3.8, #2,3,13,15
-
S-S, section 3.9, #3
-
Doing all the rest of them would prepare you even better!
Due Thursday, 17 February
Reading
-
Stein-Shakarchi, chapter 3
Lecture pictures
Exercises
Do all problems on
the first test
that you did not hand in at the time.
Due Thursday, 24 February
Reading
-
Stein-Shakarchi, chapter 3-4
Lecture pictures
-
15 February
-
17 February
-
22 February (includes scan of exercises).
Note: The final argument, about the analyticity and
bound of the Fourier transform of f, of moderate decrease,
was incorrect. It will be corrected on Thursday.
Exercises
Work out at least three and hand them in.
We can begin Thursday with a discussion of the problems.
-
Consider the transcendental equation
Use Rouché's theorem to determine the number of solutions of this
question. Distinguish among real roots and complex roots, and between the cases
a < 1 and
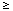 1.
1.
Hint:
Consider a large square bounded by N 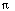 ( ± 1 ± i).
( ± 1 ± i).
For the solution, click
here.
-
S-S, section 3.8, #9, 12, 14, 20, 21
For a solution to Problem 9,
click
here.
-
S-S, section 3.9 #3 (if I fail to do this in class on Tuesday),
Due Thursday, 3 March
Reading
Lecture pictures
Exercises
Due Thursday, 10 March
Reading
-
Stein-Shakarchi, 4, Appendix B
Lecture pictures
-
29 February
-
3 March
This contains only the part about Fourier and Hermite. The rest of the
lecture consisted in working through S-S section 4.3, back to front.
Exercises
Due Thursday, 17 March
There is a scheduled test on this date.
Reading
Exercises
Due Thursday, 1 April
Reading
-
S-S, Chapter 5
-
Lecture notes from
15 March, by Prof. Croot (corrected).
-
Lecture notes from
26 March
Exercises
None due this week, and that is no April Fool's joke!
Due Thursday, 8 April
Reading
Exercises
Due Thursday, 15 April
Reading
Exercises
-
S-S, section 5.6, #5,6, 10(a).
Due Thursday, 21 April
Reading
Exercises
Homework will no longer be collected, only suggested. Feel free to
discuss it in class.
-
Prove the formula for Γ(2 z) stated in class on Tuesday, 19 April.
(Basically same as S-S section 6.3, #3.)
-
S-S, section 6.3, # 5,13,14
-
S-S, section 8.5, # 10,13,14,
Link to:
THIS PAGE IS NOT A PUBLICATION OF THE GEORGIA
INSTITUTE OF TECHNOLOGY AND THE GEORGIA INSTITUTE
OF TECHNOLOGY HAS NOT EDITED OR EXAMINED
THE CONTENT. THE AUTHOR(S) OF THE PAGE ARE SOLELY
RESPONSIBLE FOR THE CONTENT.
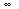 ak zk
has radius of convergence r > 0,
ak zk
has radius of convergence r > 0,
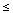 ρ < r,
ρ < r,
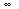 ak zk = O(zn).
ak zk = O(zn).
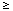 1.
1.
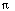 ( ± 1 ± i).
( ± 1 ± i).